三分钟彻底理解图像高斯模糊
卷积
在谈及高斯模糊之前,先了解图像处理中的一个基础操作——卷积。《Unity Shader入门精要》一书中对卷积操作有如下描述:
在图像处理中,卷积操作指的就是使用一个卷积核(kernel)对一张图像中的每个像素进行一系列操作。卷积核通常是一个四方形网格结构。(例如3X3的方形区域),该区域内每个方格都有一个权重值。当对图像中的某个像素进行卷积时,我们会把卷积核的中心放置于该图像上,依次计算核中每个元素和其覆盖的图像像素值的乘积并求和,得到的结果就是该位置的新像素值[1]。
下图[2]形象地表现了这个过程:

用公式表示卷积这个操作,在离散域上,有:
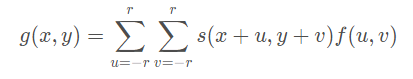
其中,(x,y)表示二维图像像素点的坐标,g(x,y)标识该像素被处理完后的像素值。r表示卷积核半径。s(x,y)表示该像素点原来的像素值。f(u,v)表示卷积核的在u,v上的权重值。f函数通常也称作滤波函数。
简而言之,卷积就是一个函数在另一个函数上的加权叠加。
模糊
模糊,就是对图像进行平滑化处理。平滑化处理,就是用平滑滤波函数,生成卷积核对应的权重,然后对图像进行卷积操作。平滑滤波函数很多,包括均值滤波函数,高斯滤波函数等。
为方便理解,先看看均值滤波函数:
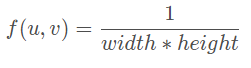
其中,width以及height分别为卷积核的宽与高。从公式可知,图像中某点的像素值就是该像素卷积核范围内的像素的均值。这就很好理解图像为什么模糊了。并且卷积核的范围越大,图像就越模糊。
至此,我们理解了模糊的过程,那么什么是高斯模糊?为什么要选用高斯模糊?
高斯模糊
高斯模糊,便是使用高斯分布作为滤波函数。我们先回顾一下高斯分布,下式为一维高斯分布的概率密度函数:
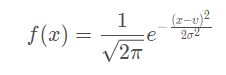
下图[3]为一维高斯分布函数图像:
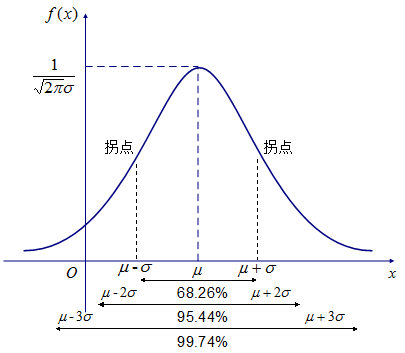
从图中可知,x距离upsilon越近,则f的值越大,越接近峰值。sigma的值越大,则峰值的值越小,函数图像越接近平稳。
对应到图像处理中,常理让我们知道,距离某像素a越近的像素,它对a的影响越大,应当越重要,因此应该有越高的权重,这和高斯分布的函数图像是吻合的。
由于图像是二维的,因此需要二维的高斯分布,其对应的概率密度函数如下:
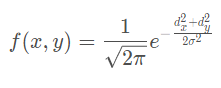
这里,dx,dy分别对应当前横竖坐标到卷积核中心的距离。
关于高斯模糊的代码实现,具体代码可以参考链接: shader,script
该实现在运算上进行了两点优化
- 缩小图像,再进行卷积操作
- 把二维高斯卷积,拆成了两个一维高斯的卷积操作(先在水平做卷积,再在垂直做卷积)
第一个优化点很好理解,这里主要补充,为什么二维高斯卷积操作,可以拆分成两个一维高斯的卷积操作。 设f(x,y),f(x),f(y)符合标准正太分布,即upsilon为0,sigma为1.有
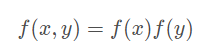
则:
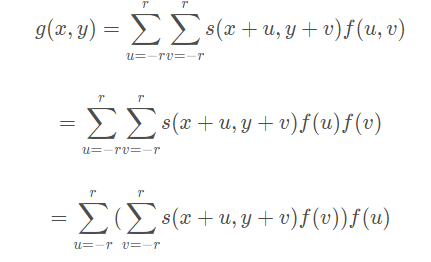
可见,先在水平方向上做一维卷积,再在垂直方向上做一维卷积,二维高斯卷积操作得以拆分。(注,上述公式忽略了对权重的归一化,实际上,应该最生成的权重进行归一化,使他们的和为1,否则亮度会降低)
[1]: 《Unity Shader入门精要》
